Muchas veces, la actualidad económica va en contra de la lógica y las primeras impresiones son las erróneas. Pese a que estamos muy acostumbrados a las estadística, no la entendemos bien y debemos intentar hacer siempre un análisis más crítico para evitar caer en las trampas de ver un simple número.
Para ello, os traigo varios juegos estadísticos bastante conocidos que os harán dudar de los datos y de vosotros mimos.
La paradoja del cumpleaños
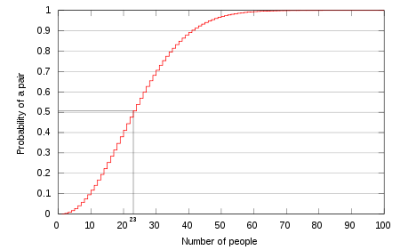
Diriges una oficina con 23 empleados. ¿Cuál es la probabilidad de que dos de ellos cumplan años el mismo día? A los efectos del problema, no consideraremos el 29 de febrero.
Respuesta: 50%
Asumiendo que es igualmente probable cada fecha de cumpleaños, resulta que cuando hay 57 personas en la oficina hay un 99% de posibilidades de que dos de ellas compartan cumpleaños. Cuando hay 23 personas la probabilidad es del 50%.
Esta es la razón. En lugar de calcular la probabilidad de que dos personas compartan la fecha de cumpleaños, calcula lo inverso, la probabilidad de que dos personas no hayan nacido el mismo día. Dado que estas situaciones son mutuamente excluyentes, la primera probabilidad más la segunda tiene que ser igual a 1.
Así es como se calcula.
Elige a dos personas de la oficina. La probabilidad de que la segunda no haya nacido el mismo día que la primera es de 364/365. La probabilidad de que la tercera persona no haya nacido el mismo día que la primera o la segunda es de 363/365. Siguiendo con el resto de la oficina y multiplicando todo esto, se comprueba los siguiente:
365/365 x 364/365 x 363/365 x 362/365 x … x 343/365 = 0,4927.
Por tanto, la probabilidad de que ninguna persona de una oficina de 23 comparta la fecha de cumpleaños es de 0,4927 o del 49,3%. Eso significa que la probabilidad de que dos personas de la oficina hayan nacido el mismo día es igual a 1 — 0.4927 = 0,5073 o del 50,7%.
En este caso, la respuesta va en contra de la lógica y la solución está en mirar las cosas desde un punto de vista completamente distinto.
La ruina del jugador
Este sistema es un clásico en los jugadores de ruleta (su nombre es la martingala) y tambiém de muchos inversores en bolsa (ellos lo llaman promediar). Consiste en doblar la apuesta cuando se pierde para recuperar siempre lo que has perdido.
Por ejemplo, vamos a la ruleta y apostamos siempre a rojo. Empezamos apostando un euro, si ganamos, seguimos apostando la misma cantidad pero si perdemos apostamos el doble para recuperar lo perdido.
Si sigues así, ¿cuál es el beneficio esperado?
Respuesta: lo perderás todo
En Microsiervos lo explicaron muy bien hace años.
El método de «ir doblando las apuestas cuando se pierde, para recuperar siempre más de lo perdido» no funciona para hacerse rico en los casinos. Normalmente se aplica a juegos con apuestas tipo dos-a-uno como la ruleta (jugando a Rojo/Negro, Par/Impar o similares). Lo que sucede al emplear este sistema que es que, aunque a veces se pueda ganar algo de dinero tras varias apuestas (gracias a la aparente «recuperación» por doblar la apuesta cuando se pierde) y aunque parezca «obvio» que se puede repetir y repetir el método sesión tras sesión, día tras día para ganar más y más, a la larga no funciona, por varios factores correlacionados:
Primero, las mesas tienen un límite de apuesta. Segundo, el dinero de que dispone el jugador no es infinito. Y tercero, y más importante, las secuencias largas de varios resultados negativos acaban apareciendo a largo plazo. Cuando alguna de estas cosas sucede (no se puede apostar más del límite para recuperar, el jugador se queda sin dinero real con el que apostar, y todo ello tras una de esas «rachas negativas» que acaban apareciendo) el jugador lo pierde todo. Fin del juego.
Por otro lado, no debemos olvidarnos de que si alguien participa en juegos de azar durante suficiente rato, siempre y cuando se enfrente a un oponente más rico que él (bien sea un casino o, por qué no, la bolsa), si sigue apostando contra un adversario mucho más rico que él, la probabilidad de perder acaba llegando al 100% al cabo de un tiempo. Desgraciadamente nos ciegan las expectativas de beneficio y el creernos más listos que los demás.
Muchas veces olvidamos lo rápido que se pueden disparar las deudas, por ejemplo, con este método de apostar sólo un eurito y duplicar si pierdes se queda en que la apuesta tras perder 14 jugadas seguidas son más de 8.000 euros , con 15 son 16.000… con 18 resultados en contra se supera la barrera de los 100.000 euros, y con 21 la del millón de euros.
El problema Monty Hall
Digamos que estamos en un concurso de televisión en el que hay tres puertas. Detrás de dos de las puertas hay cabras. Detrás de la tercera hay un coche nuevo.
El presentador dice que cuando elijas una de las puertas abrirá otra que no has elegido para mostrar a las cabras. Después, puedes quedarte con tu puerta o cambiarla por la otra de las puertas que no está abierta.
¿La abrirías o cambiarías de puerta?
Respuesta: cambiar
Está basado en un concurso real, y el resultado ha sido fuente de controversia durante años.
En esencia, cuando eliges al principio tienes una opción entre tres de seleccionar la puerta correcta con el coche detrás. Cambiar de puerta después eleva esa probabilidad a dos entre tres.
Dicho de otro modo: un jugador cuya estrategia es cambiar siempre, únicamente perderá cuando la puerta que haya elegido al principio tuviera el coche detrás. Un concursante que elija cualquiera de las dos puertas con una cabra detrás y que después cambie de puerta siempre ganará el coche.
Aquí hay otra manera de verlo, siempre que el concursante eligiese la puerta nº 1
Puerta 1 Puerta 2 Puerta 3 Resultado si nº1 Resultado si cambia
Coche Cabra Cabra Coche Cabra
Cabra Coche Cabra Cabra Coche
Cabra Cabra Coche Cabra Coche
En este problema, la estadística colabora con nosotros y conviene fiarse de ella más allá de las corazonadas que podamos tener.